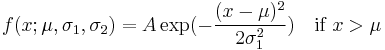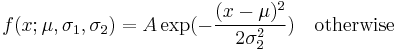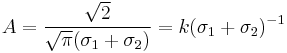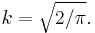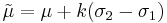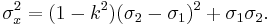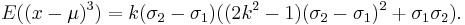Split normal distribution

In probability theory and statistics, the split normal distribution also known as the two-piece normal distribution results from joining at the mode the corresponding halves of two normal distributions with the same mode but different variances. The split normal distribution was introduced by Gibbons and Mylroie[1] and by John.[2]

Contents

Definition

The probability density function of the split normal distribution is given by[3]

f(x;\mu,\sigma_1,\sigma_2)= A \exp (- \frac {(x-\mu)^2}{2 \sigma_1^2}) \quad \text{if } x> \mu
f(x;\mu,\sigma_1,\sigma_2)= A \exp (- \frac {(x-\mu)^2}{2 \sigma_2^2}) \quad \text{otherwise}

where

A=\frac {\sqrt{2}} {\sqrt{\pi}(\sigma_1%2B\sigma_2)}= k (\sigma_1%2B\sigma_2)^{-1}

where

k = \sqrt{2 / \pi} .

Moments and other properties

The parameter μ is the mode of the distribution (unlike for the Normal distribution, where μ is both mode, mean and median). The split-normal distribution has the following moments:

mean:

\tilde{\mu} = \mu%2Bk(\sigma_2-\sigma_1)

variance:

\sigma^2_x = (1-k^2)(\sigma_2-\sigma_1)^2 %2B \sigma_1 \sigma_2 .

The third central moment is given by:

E((x-\mu)^3) = k(\sigma_2-\sigma_1)((2k^2-1)(\sigma_2-\sigma_1)^2 %2B \sigma_1 \sigma_2).

The sign of the third central moment is determined by the dfference in sigmas (the second factor in the formula above). If this difference is positive, the distribution is skewed to the right and if it is negative, to the left.

In a special case where 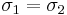\sigma_1 = \sigma_2 , the split normal density collapses to the density of the Normal distribution.

Other properties of the split normal density have been discussed by Johnson et al.[3] and Julio.[4]

Applications

The split normal distribution has been used mainly in econometrics and time series. A remarkable area of application is the construction of the fan chart, a representation of the inflation forecast distribution reported by inflation targeting central banks around the globe.[4][5]

References

  1. ^ Gibbons, J.F.; Mylroie, S. (1973). "Estimation of impurity profiles in ion-implanted amorphous targets using joined half-Gaussian distributions". Applied Physics Letters 22: 568–569. 
  2. ^ John, S. (1982). "The three-parameter two-piece normal family of distributions and its fitting". Communications in Statistics - Theory and Methods 11 (8): 879–885. http://www.informaworld.com/10.1080/03610928208828279. Retrieved 2011-03-09. 
  3. ^ a b Johnson, N.L., Kotz, S. and Balakrishnan, N. (1994). Continuous Univariate Distributions, Volume 1. John Wiley & Sons. p. 173. ISBN 0-471-58495-9. 
  4. ^ a b Juan Manuel Julio (2007). "The Fan Chart: The Technical Details Of The New Implementation". Banco de la República. http://ideas.repec.org/p/col/000094/004294.html. Retrieved 2010-09-11, direct link 
  5. ^ Bank of England, Inflation Report